가상 데이터 만들어 기본 머신러닝 알고리듬 적용하기
파이썬으로 머신러닝 프로그래밍을 하려면 어떻게 해야 할까요? 일단 머신러닝을 할 데이터가 있어야 하겠습니다. 그런 다음 머신러닝의 어떤 알고리듬을 사용해야할지 결정해야겠습니다.
머신러닝에는 여러 알고리듬이 있습니다. 대부분의 알고리듬은 직접 처음부터 프로그래밍을 할 필요 없습니다. 이미 파이썬에서 쓸 수 있게 프로그래밍이 되어 있고, 이를 모듈이나 패키지로 만들어 놓았습니다. 그러면, 그런 모듈이나 패키지를 어디에서 찾을 수 있을까요? 알고리듬마다 일일히 모듈이나 패키지를 찾아야 할까요?
다행히도 딥러님과 강화학습을 제외한 머신러닝 알고리듬 대부분은 한 패키지안에 모여 있습니다. scikit learn이라는 패키지입니다. 만약에 머신러닝으로 뭔가 하고 싶으면 scikit learn만 설치하고 불러오면 웬만한 건 다 해결할 수 있다는 얘기입니다. 그리고 아나콘다(anaconda)로 파이썬을 설치했으면 scikit learn도 이미 설치되어 있습니다. 따라서 바로 프로그래밍을 하면서 불러오기만 하면 됩니다.
이제 가장 기본적인 머신러닝 알고리듬인 Linear Regression이라는 알고리듬을 적용해 보겠습니다. 그러기 위해 scikit learn페기지안에 있는 linear_model 모듈을 불러올겁니다. 이 모듈안에 Linear Regression 이라는 알고리듬이 들어있기 때문입니다. 그리고 scikit learn 패키지 이름은 sklearn 이어서, 다음과 같은 코드를 실행해야 linear_model을 불러올 수 있습니다.
from sklearn import linear_model
이제 linear_model안에 있는 알고리듬을 쓸 준비가 되었습니다. 우리가 해볼려고 하는 Linear Regression 알고리듬을 쓸려면 아래의 코드를 실행해야 합니다.
reg = linear_model.LinearRegression()
linear_model안에 있는 LinearRegression이라는 함수를 실행해 그 결과를 reg라는 변수에 저장한 것처럼 보입니다. 하지만 이건 함수를 실행한 것이라기 보다는 클래스 객체를 만든 것입니다. 간단하게 설명하면, 클래스는 특정 작업을 하는 함수들과 변수들을 정해 놓은 일종의 설명서입니다. 클래스 객체는 클래스가 정해놓은 설명서대로 일을 하는 일종의 일꾼입니다.
위의 코드에서는 reg라는 변수에 LinearRegression이라는 설명서대로 일꾼을 만들어 저장하는 것이라고 보면 되겠습니다. Linear Regression을 하는 일꾼을 만들어 놓았으니 이제 이 일꾼에 일을 시킬 준비만 하면 됩니다.
지난 자료에서 만들었던 가상 데이터를 약간 변형해서 머신러닝 알고리듬에 적용하기 위한 데이터로 만들어 보겠습니다.
import random random.seed(1) datalen = 200 x1 = [ random.gauss(5.0, 2.0) for k in range(datalen) ] x2 = [ random.gauss(5.0, 2.0) for k in range(datalen) ] y = [ x1[k]+random.gauss(0.0, 0.5) for k in range(datalen) ]
지난 자료에서 난수를 만드는데 random.random()이라는 함수를 사용했었습니다. 0에서 1사이에서 숫자의 크기와 상관없이 같은 확률로 숫자를 무작위로 만드는 함수였습니다. 위의 코드에 쓴 random.gauss(5.0, 2.0) 함수는 5를 만들 확률이 가장 크고 5에서 멀어지는 숫자일수록 만들 확률이 종(bell)모양으로 적어지는 방식으로 무작위 숫자를 만드는 함수입니다. 이 함수의 두번쨰 입력값이 크면 더 넓은 숫자 범위에서 난수를 만들고, 두번쨰 입력값이 작으면 더 좁은 숫자 범위에서 난수를 만듭니다. 세번째줄에 random.seed(0)을 쓴 이유는 위의 코드를 누가 써도 같은 결과가 나오게 하기 위해서 입니다.
이렇게 만든 $x_1$ 목록의 값들을 가로축에 놓고 $y$ 목록의 값들을 세로축에 놓고 점을 찍으면 아래와 같은 그래프가 만들어집니다.
import matplotlib.pyplot as plt %matplotlib inline plt.rcParams['figure.dpi'] = 150 plt.plot(x1, y, "x")

$x_1$목록안의 숫자가 작으면 $y$ 목록안의 숫자도 작고, $x_1$목록안의 숫자가 크면 $y$ 목록안의 숫자도 큰 식으로 서로 연관되어 있습니다.
반면 아래와 같이 $x_2$ 목록의 값들과 $y$ 목록의 값들로 그래프를 그리면, 두 목록의 값들이 상하좌우로 넓게 퍼져 서로가 별로 연관되어 있지 않음을 알 수 있습니다.
plt.plot(x2, y, "x")

이렇게 만든 데이터를 가지고 scikit learn의 Linear Regression 알고리듬을 적용해보겠습니다. $x_1$과 $x_2$ 목록을 입력 데이터로, $y$ 목록은 결과 데이터로 사용하려고 합니다.
그런데 scikit learn안에 있는 알고리듬을 적용하려면, 입력데이터가 표의 형식을 하고 있어야 합니다. 목록의 목록 다시 말해 2차원 목록의 형식을 하고 있어야 한다는 의미입니다. 위의 코드로 만든 데이터중에 $x_1$와 $x_2$를 입력 테이터로 쓰려면 다음과 같은 형식으로 바꿔야 합니다.
$$ X = \left[
\begin{array}{c} [\ x_1[0],\ x_2[0]\ ], \\ [\ x_1[1],\ x_2[1]\ ], \\ \vdots \\ [\ x_1[99],\ x_2[99]\ ] \end{array}
\right] $$
이를 파이썬 코드로 만들면 다음과 같습니다.
X = [ [x1[k], x2[k]] for k in range(datalen)]
scikit learn의 LinearRegression 클래스를 쓸때, 결과 데이터는 목록의 형식을 하고 있어야 합니다. 따라서 y를 그냥 그대로 쓰면 되겠습니다.
우리가 하려는 머신러닝 작업은 결과 데이터 $y$를 입력 데이터 $x_1$과 $x_2$에 숫자만 곱해서 더하는 방법으로 표현하려는 것입니다. 수식으로 쓴다면
$$ y = a_0+a_1x_1+a_2x_2$$
이 되겠습니다.
입력데이터와 결과데이터가 준비된 상황에서는 이 작업을 아래의 코드로 할 수 있습니다.
reg.fit(X, y)
함수 fit은 위의 수식을 데이터에 최대한 가깝게 맞춰나가는 일을 합니다. 그래서 데이터를 가장 잘 표현하는 $a_0$, $a_1$, $a_2$를 찾아 위의 수식을 완성하는 겁니다. 머신러닝에서는 컴퓨터가 “학습한다”고 말합니다.
계산 결과는 reg라는 클래스 객체안에 있는 변수에 저장됩니다. $ y = a_0+a_1x_1+a_2x_2$ 에서 $a_0$ 값은 reg.intercept_에 숫자로, $a_1$과 $a_2$ 값은 reg.coef_에 목록으로 저장됩니다. 이를 알아낼려면 아래의 코드를 실행하면 됩니다.
print(reg.intercept_) print(reg.coef_)
출력 결과는 아래와 같습니다.
-0.145468456244 [ 1.0134866 0.00665415]
수식으로 표현하면
$$ y = -0.1455+1.0135x_1+0.0067x_2 $$
이 되겠습니다.
그런데 가상 데이터를 만들때 이미 알 수 있듯이 $y$값은 $x_1$과 연관되어 있지만 $x_2$와는 별로 연관되어 있지 않습니다. $x_2$와 $y$를 그린 그래프에서 전들이 넓게 퍼진 것과 $a_2$의 값이 아주 작은 것만 봐도 알 수 있습니다.
그러면 입력 데이터에서 $x_2$는 제외하고 $x_1$만 써서 알고리듬을 적용해 보겠습니다.
$$ y = a_0+a_1x_1$$
입력 데이터가 $x_1$ 하나 밖에 없어도, 입력데이터 형식은 2차원 목록(목록의 목록) 형식으로 준비해야합니다. 입력데이터로 가공하고 알고리듬을 적용해 계산결과를 보면 다음과 같습니다.
X = [ [ x1[k] ] for k in range(datalen)] reg.fit(X, y) print(reg.intercept_) print(reg.coef_)
출력 결과는 다음과 같습니다.
-0.108736225652 [ 1.01303793]
수식으로 표현하면
$$ y = -0.1087+1.0130x_1 $$
이전의 $a_0$와 $a_1$값과 별로 차이나지 않습니다.
$x_1$과 $y$를 그래프에 동그라미모양의 점으로 찍고, 알고리듬 적용 결과 $ y = -0.1087+1.0130x_1 $을 선으로 그려보면 다음과 같습니다.
a0 = reg.intercept_ a1 = reg.coef_[0] import matplotlib.pyplot as plt %matplotlib inline plt.rcParams['figure.dpi'] = 150 plt.plot(x1, y, "x") xplot = [ k*0.1 for k in range(100) ] yplot = [ a0+a1*xplot[k] for k in range(100)] plt.plot(xplot, yplot)

이제 새로운 입력 값이 있으면 그 입력값으로 어떤 결과가 나오는지를 예측할 수 있습니다.
$$ y = -0.1087+1.0130x_1 $$
으로 바로 계산할 수 있기 때문입니다.
만약에 1, 2, 3, … , 10 입력값에 대한 결과를 예측하려면 입력값의 2차원 목록을 만들어 다음과 같은 코드를 실행하면 됩니다.
xp = [ k for k in range(11) ] Xpred = [ [xp[k] ] for k in range(11) ] ypred = reg.predict(Xpred) print(Xpred) print(ypred)
출력 결과는 다음과 같습니다.
[[0], [1], [2], [3], [4], [5], [6], [7], [8], [9], [10]] [ -0.10873623 0.9043017 1.91733963 2.93037757 3.9434155 4.95645343 5.96949136 6.98252929 7.99556722 9.00860515 10.02164308]
위에 예측한 결과를 모델로 찾아낸 직선과 함께 그래프로 그려보겠습니다.
plt.plot(xp, ypred, "s") plt.plot(xplot, yplot)
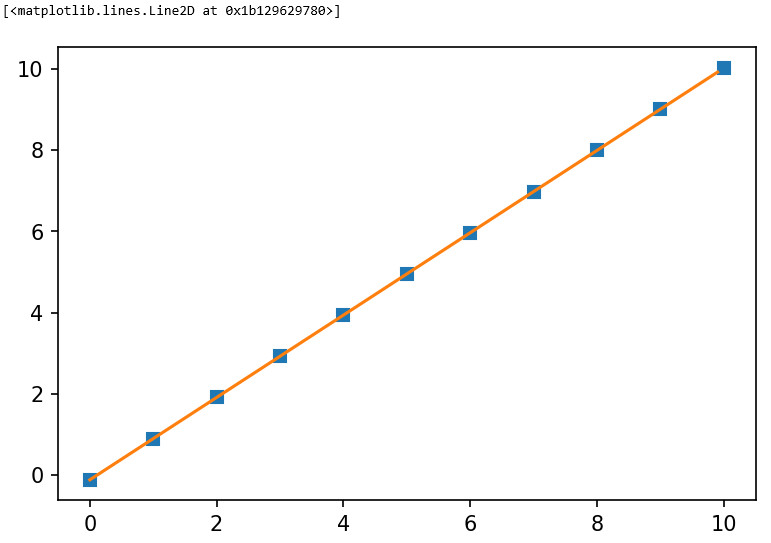
위의 그래프와 같이 예측한 값은 직선 위에 있습니다. 직선이 바로 예측을 하는데 쓰는 수식을 그래프로 그린 것이기 때문입니다.